Что такое Лента Мебиуса?
Лента Мёбиуса (или ее также называют кольцом Мёбиуса, лентой Мёбиуса и даже кольцом Мёбиуса) — одна из самых известных поверхностей в математике. Петля Мебиуса — это петля с поверхностью и ребром.
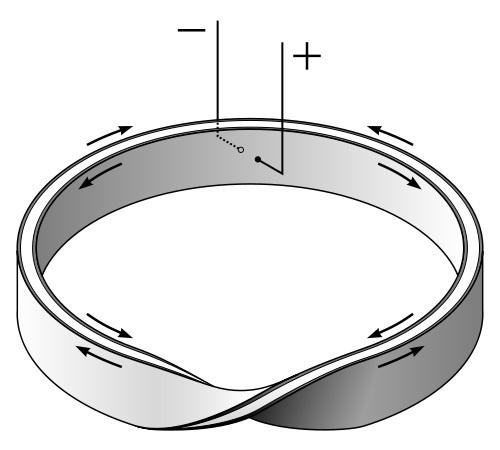
Чтобы понять, о чем идет речь и как это может быть, возьмите лист бумаги, вырежьте прямоугольную полоску и, когда придет время соединять концы, поверните одну из них на 180 градусов, затем соедините. Изображение ниже поможет вам понять, как сделать ленту Мебиуса.
Что же такого примечательного в ленте Мебиуса?
Лента Мебиуса является примером односторонней неориентируемой поверхности с ребром в обычном трехмерном евклидовом пространстве. Большинство объектов ориентируются и имеют две стороны, как лист бумаги.
Как же тогда лента Мебиуса может быть односторонней и неориентируемой поверхностью — скажете вы, потому что бумага, из которой она сделана, имеет две стороны. Но вы пытаетесь взять маркер и заполнить одну сторону ленты цветом, в конце концов вы побежите в исходное положение, и вся лента будет полностью окрашена, что подтверждает, что у нее только одна сторона.
Чтобы поверить в то, что петля Мебиуса имеет только один край, проведите пальцем по одному из краев ленты без прерывания и, как и в случае с раскрашиванием, вы натолкнетесь на то место, где начали движение. Невероятно, правда?
Изучением ленты Мёбиуса и многих других интересных объектов занимается — топология, раздел математики, изучающий неизменные свойства объекта при его непрерывной деформации — растяжении, сжатии, изгибе, не нарушая его целостности.
Открытие Августа Мебиуса
«Отцом» первооткрывателя этой необычной ленты является немецкий математик Август Фердинанд Мебиус, ученик Гаусса, который написал не одну работу по геометрии, но прославился открытием односторонней поверхности в 1858 году.

удивительно, что лента с поверхностью в том же 1858 году была обнаружена другим учеником Гаусса — талантливым математиком Иоганном Листингом, который ввел термин «топология» и написал ряд фундаментальных работ по этому разделу математики. Однако необычная лента до сих пор носит название Мёбиуса.

распространено мнение, что прототипом модели «бесконечной петли» послужила неправильно сшитая ленточка слугой профессора Августа Мебиуса.
На самом деле лента была обнаружена очень давно в древнем мире. Одно из подтверждений — древнеримская мозаика с такой же витой лентой, находящаяся во Франции, в музее города Арля. Он представляет Орфея, животных, очарованных звуками арфы. На заднем плане неоднократно изображен орнамент с перекрученной лентой.

«Магия» ленты Мебиуса
- Несмотря на кажущееся наличие двух сторон у ленты Мебиуса, на самом деле сторона только одна, и для покраски ленты в два цвета она не подойдет.
- Если вы проведете линию по всей длине петли ручкой или карандашом, не отрывая руки от бумаги, отвес в конечном итоге остановится там, где вы начали рисовать линию;
- Замечательные впечатления получаются от перерезания ленточки, способной удивить и взрослого, и, в частности, ребенка.
- Сначала приклеим ленту Мебиуса, как описано выше. Затем вырезаем его по всей длине ровно посередине, как показано ниже:

Результатом вы удивитесь, ведь вопреки ожиданиям в ваших руках останутся не два отрезка скотча и даже не два отдельных кружочка, а еще один скотч еще большей длины. Это будет уже не лента Мебиуса, скрученная на 180 градусов, а лента с поворотом на 360 градусов.
- Теперь проведем еще один эксперимент: сделаем еще одну петлю Мебиуса, после чего отмерим 1/3 ширины ленты и разрежем по этой линии. Результат поразит вас еще больше: в ваших руках останутся две отдельные ленты разного размера, соединенные между собой, как в цепочку: одна небольшая лента и одна вторая длиннее.

Полоса Мебиуса меньшего размера будет иметь 1/3 ширины исходной полосы, длину L и угол поворота на 180 градусов. Вторая по длине лента также будет иметь ширину 1/3 от начальной, но длину 2L и угол поворота на 360 градусов.
- Вы можете продолжить эксперимент и дальше, разрезав получившиеся ленты на еще более узкие, вы сами увидите результат.
Зачем нужна петля Мебиуса? Применение
Лента Мебиуса отнюдь не абстрактная фигура, она нужна только для целей математики, она нашла применение в реальной повседневной жизни. По принципу этого ремня в аэропорту действует ремень, перемещающий чемоданы из багажного отделения. Такая конструкция позволяет ему прослужить дольше за счет равномерного износа. Открытие Августа Мёбиуса широко используется в станкостроении. Эта конструкция используется для увеличения времени записи на ленту, а также в принтерах, использующих ленту для печати.
Благодаря своей ясности цикл Мебиуса позволяет современным ученым делать все больше и больше открытий. С момента открытия необычных свойств кольца по всему миру распространилась волна новых запатентованных изобретений. Например, значительное улучшение свойств магнитопроводов, изготовленных из ферромагнитной ленты, намотанной по методу Мебиуса.
Н. Тесла получил патент на многофазную систему переменного тока, использующую обмотку катушек генератора по типу кольца Мебиуса.
Американский ученый Ричард Дэвис разработал нереактивный резистор Мебиуса, способный гасить реактивное (емкостное и индуктивное) сопротивление, не вызывая электромагнитных помех.